杰出科学世家——伯努利家族恩仇录

►伯努利兄弟

撰文 | 洪蔚琳

当丹尼尔·伯努利带着巴黎科学院的大奖回到家乡，父亲约翰只做了一个决定：把儿子赶出家门。这一年，父子俩各自提交论文，最终共享殊荣，但这只会激起约翰的懊恼。关上房门，约翰料定，这是儿子刻意为他设下的圈套，想与他平起平坐。如此奇耻大辱，他一生都不会原谅。

这是1734年，牛顿已长眠地下。在失去所有对手后，约翰·伯努利终于成为这个时代最举足轻重的数学家。他在日记中傲然写道：“我的对手们都死在我前面，而且都比我年轻，这是一种命运。”他一人站在高峰，纵然孤独，却不允许任何人夺去他的光芒，哪怕是他自己的后代。

没有人能解释，是什么造就了伯努利家族。从十七、十八两世纪以来，伯努利家族三代人中出现了八位卓越的科学家，在微积分的发展和应用上扮演领导角色，推动整个世界科学史翻过划时代的一页。但与科学光辉相对的，是家族内部从未平息的纷争。当智慧与激情代代相传，流动在伯努利家族血液中的，还有名垂青史的野心和独揽荣耀的欲望。

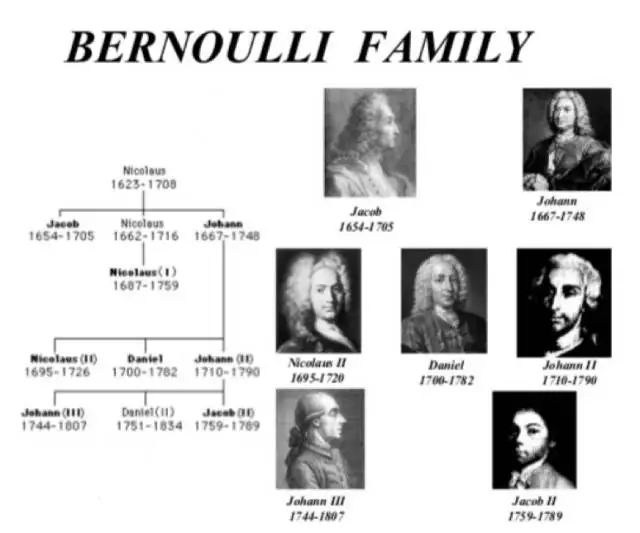
►伯努利家族谱系表

像酒鬼碰到烈酒

老尼古拉·伯努利失去了一切指望，他没能阻止大儿子雅各布投身数学，如今小儿子约翰也要走上哥哥的老路。那时他无法预料，两兄弟日后将成为欧洲大陆首屈一指的数学大师，他满脑子都是家道或将中落的伤感。

可以想像，这个新教家族离开安特卫普，在战火中经历长达50年的逃亡，才终于定居在瑞士巴塞尔。几代先祖经商，并与商人的女儿结婚，才终于累积起大量财富。优先学习商科，其次是神学与医学，成为伯努利家族代代相传的家训。怎么到了这一代，情况就变了呢？后世将伯努利兄弟对数学的狂热调侃为“像酒鬼碰到了烈酒”。老尼古拉想不通，贫苦的数学生涯究竟有什么值得追求。

无论如何，17世纪的漫游之风让雅各布跳出家族传承的框架。在取得神学硕士学位后，他和当时的众多青年一样，骑马去游历。从日内瓦到法国、荷兰、英国，他在途中一边传道，一边做数学家教。在宽松的环境下，他自学笛卡尔的自然哲学，写下200余篇关于数学的日志。六年后回到巴塞尔，他再也不想去做神职人员，只想钻研数学。巴塞尔大学为他提供了教职，他开始在授课之余，定期向数学杂志投稿。

哥哥的经历究竟对约翰意味着什么？在他入读巴塞尔大学的那一年，雅各布刚好回到家乡。眼见着长子辜负了家族的期望，老尼古拉把光耀门楣的全部责任压在约翰肩头。这个孩子看上去聪明、外向，是父母眼中经商的好苗子。老尼古拉不遗余力地向他灌输道德与宗教——在新教伦理中，努力挣钱即道德。约翰长到15岁，就被父亲安排进入家族商行做学徒。他心底的声音从来没有得到尊重：他厌恶商业，他也喜欢数学。

哥哥的任性无疑为约翰带来了更沉重的压力，但也为他的选择做了榜样。一年后，约翰以攻读医科作幌子，勉强说服父亲让他去读大学。他似乎比哥哥更善于搭建自己的人际网。短短几年，他和莱布尼茨、医学著作家Daniel Leclerc、哲学家尼古拉斯.马勒伯朗士成了朋友、并通过马勒伯朗士结识洛必达侯爵，在接下来漫长的数十年中担任侯爵的数学老师。在巴塞尔大学，他最终向父亲显示了自己远超医学之外的，真正的兴趣和野心：他把微积分应用于肌肉收缩，因此获得医学博士学位。这项工作在数学领域同样有分量。

►雅各布·伯努利（左）与约翰·伯努利（右）

裂痕

洛必达侯爵在1696年收到约翰的来信，信中写道：“你不会相信，我这个哥哥是多么名不副实。他恨我，迫害我，试图摧毁我….他看上去对我温和友好，心里却暗藏毒药。”

没有一个标志性的事件，证明兄弟情谊在哪一刻戛然而止。或许一切早有端倪：十五年前，当两人同时活跃在巴塞尔大学，雅各布是教师，而约翰是学生。约翰在哥哥的指导下接触数学，他们也曾共同完成一系列卓越的研究成果，但这段关系从一开始就暗藏罅隙。

约翰在自传中写道：“那段时间，我模仿着哥哥雅各布的兴趣，认真从事数学研究。我只用了不到两年时间，就读遍所有经典数学家，还熟悉了现代大师的成果，如笛卡尔的几何学。”约翰视自己为自学者，但雅各布把弟弟当成自己的学生。在写给莱布尼茨的信中，他明确声明，约翰的全部数学基础都来自他的馈赠。

著名的悬链线之争让矛盾显化，原本处于“助手”角色的约翰第一次击败哥哥，一夜间跻身欧洲最重要的数学家行列。悬链线问题如今看来非常简单：两端固定的绳子（或链条）由于重力而自由下垂，形成的曲线到底是什么形状。在微积分和牛顿力学初建的年代，答案悬而未决。早在1638年，伽俐略错误地猜测悬链线是抛物线，八年后，17岁的少年惠更斯推翻了这个假设。但不是抛物线，又是什么线？它的方程是怎样的？最初是雅各布在期刊上建议数学界重新对问题展开研究。

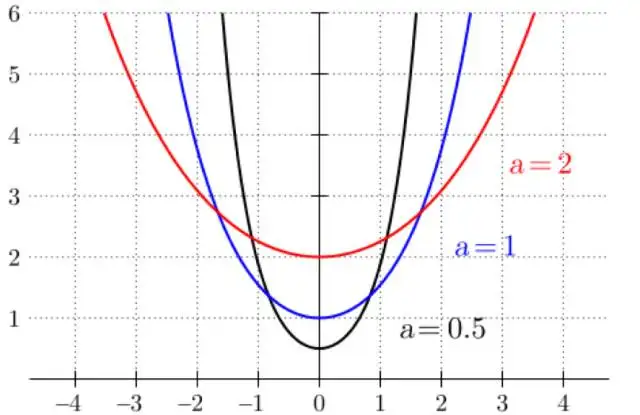
►不同的悬链线

雅各布最终收到了多个答案，其中就有来自弟弟约翰、莱布尼茨以及惠更斯。他们成功地用微积分解决了问题，证明悬链线是一个双曲余弦函数。自己提出的问题被弟弟破解，这本已令雅各布感到尴尬，而约翰抓住这个机会，四处靠贬损哥哥来抬高自己，更是激化了二人的矛盾。

直至27年后，约翰在给蒙莫尔的信中谈起此事，依旧用词轻蔑。他写道：

“哥哥的努力没有结果。而我却幸运得多……我花了一晚上来钻研它……第二天早上，我满怀喜悦地跑到哥哥那儿，他还在痛苦地思索如何解开这个戈尔蒂之结。他茫无头绪，老是像伽利略那样认为悬链线是一种抛物线。打住！打住！我对他说，不要再试图证明悬链线是抛物线来折磨你自己了，因为这完全错了……这两条曲线完全不同，一条是代数的，另一条是超越的……我向他展示我的解决方案，并发现了引导我成功的方法。”

挣脱

约翰动身去游历，先到日内瓦，然后法国…..是的，连游历路线都与哥哥出奇一致。他一面模仿着哥哥的漫游，一面渴望挣脱：他成熟了，不再甘于做个助手。也许只有远离哥哥，他才能成为独立的科学家。

通信与学术上的合作并未终止。他们探索同样的问题，不断从对方的观点中获取灵感。依旧是雅各布提出问题，两人常常同时发表文章，但不再合著，任何成果总是归于其中之一。

但约翰依旧是被动的，像被哥哥隐形的手掐住喉咙。创办于莱比锡的德意志第一份专业科学期刊《教授学报》（Acta Eruditorum）是两人刊发成果的主要阵地，但约翰却无法与《教授学报》直接沟通，一切都要靠哥哥作中介。由此引发的不愉快接二连三：约翰把一篇文章寄给哥哥，刊发后却发现哥哥在结尾自作主张地加段落，并附署名；出于难以说明的原因，哥哥有时并不会将莱比锡方面的消息转告约翰。

►《教授学报》（Acta Eruditorum）

令约翰难以容忍的是，这种无形的控制让他无法拥有专属于自己的荣耀。他常常在信中满腹牢骚：“你为什么不能多等一段时间，再发表你的发现？我已经找到了更好的方法，比你的更有普适性”；“也许你觉得我的想法全是受你启发，但我说的都是事实”；“就算我不是第一个找到它的，我应得的赞美也一点儿不该少。”诚然，如果数学界只保留第一个发现者的名字，那么第二个人还能期望得到什么认可？一个拥有同等天才的人，如何能忍受一生做他人的附庸？

雅各布似乎从未考虑过弟弟的感受。他曾把学术上的合作比喻为两个人去两个不明地点旅行，每个人都尽可能地带回东西，但没有人能拿到另一个地点的一切。因此，面对同样的问题，即使两个人都以自己的方式找到正确的解决办法，任何人都不该得到所有荣耀。这似乎是雅各布的哲学。但每每涉及具体问题，他又换了一套说辞：他才是发现新径的人，约翰只是他的跟从。

在这剑拔弩张的时刻，有关悬链线的问题再一次触发了笔战的机关。雅各布对风中船帆的形状问题产生兴趣，他寄给弟弟一个曲线的微分方程（d2x ：dx = dy3），并要求从中得出能表达曲线性质的文字或代数方程。约翰的第一反应是，船帆的曲线可以用悬链线来定义，却被哥哥否决。

雅各布考虑风影响帆的多种情形，这遭到了约翰的嘲讽：“你声称帆部分是圆的外围，部分是其他曲线的外围，怎么可能产生两条不同的曲线？你就像古人相信大炮球的轨迹有三条线。如果这不是幻觉，那它一定是普罗透斯。”他的措辞相当犀利。在旧时代，大炮的轨迹被认为是由直线和曲线组成；希腊神话中的海神普罗透斯经常变化外形，就像直线和曲线两种形态来回替换。

当约翰在巴黎旅途中，雅各布终于发现了标志性的结果：曲线确实是悬链线。但他只寄给约翰一个方程式，并未言明曲线性质。兴奋的约翰立即发现，它就是一个悬链线！他猜想哥哥并没看出这一点，便在1692年4月的期刊文章中如此调侃：“哥哥再次强迫我完成他的工作，显然，他做到方程式这一步就完全放弃了。”不幸的是，雅各布早已在3月投出他的解决方案，5月发表。

约翰自以为抓住了独立的机会，但他输了。更糟的是，这段兄弟关系从此再难修复。被激怒的雅各布决定盘点他的所有首次发现。他甚至写信给莱布尼茨，讲述他和约翰的生平以及他们早年的数学成就。他声称自己才是参透莱布尼兹微积分奥秘的第一人，约翰分享了他的果实。

宣战

战火烧到了整个数学界，几乎全世界所有最重要的数学家都收到约翰的邀请，为最速降线提出解决方案。为确保宣传的广泛性，约翰甚至在格罗宁根印刷海报。这一次，他要主动出击，打败他的哥哥。

雅各布坐在书桌前，他摊开刚刚收到的海报，淡定地笑笑。他马上提笔给莱布尼茨写信：“在这个瞬间，我把手放在一张印刷海报上。我能感觉到，我弟弟仿佛在字里行间泼上毒液。他想让世界上所有数学家解决他的问题，特别是我。”

什么形状的滑梯，能让滑动者到达地面的时间最短？这就是最速降线问题。假设A和B是地面上高低不同（A不低于B）、左右有别的两个点，一个没有初始速度的小球，在无摩擦力，只有重力的作用下从A点滑到B点。从A到B的轨道可以有很多，哪一条轨道，将使小球从A到B的时间最短？

►最速降线问题

约翰早已知晓答案，他用两个星期解决了这个问题。在收到哥哥的答案后，他立刻欢欣雀跃。无可争议！我的答案简洁漂亮，而哥哥的答案是最笨最差的。他再次单方面宣告了自己的胜利，但事实果真如此么？

约翰的答案的确简洁，因为他借用了光学中费马的光程最短原理。法国数学家费马研究光学时发现，光线在两点间的实际路径是使所需的传播时间为极值的路径。在大部分情况下，此极值为最小值，但有时为最大值，有时为恒定值。换言之，光线传播的经典路径是变分为0的路径。约翰用光线类比小球，导出了最短路径所满足的微分方程。他的答案没错，却是一种投机取巧，因为他当时无法论证这种做法的正确性。

雅各布的方法很繁复，却在推导中闪烁出新的变分思想的光辉。他首先假设小球沿着最速路径下滑，然后考虑：如果在某个时刻，小球的路线稍微偏离了最速路径，会发生什么情况？上述做法已经是一种变分的思想，因为他是在考虑所有微小偏离路径中使得时间最小的那个偏离。然后，雅各布用二阶导数的方法证明，为使小球继续走时间最短的路，它的路线的微分偏离量应该满足的方程，刚好是摆线所满足的微分方程。

恩斯特·马赫曾如此评价两兄弟：“他们一个有艺术家一般的直觉与激情，一个有批判性的思维纵深。这是天才的两面，如果结合在同一个人身上，就会造就伟大的科学家。可惜这两面分开了，那么冲突就是必然。”

这是多么精辟的评点！雅各布心思缜密，个性沉稳，他总是通过解决应用数学的具体问题，来发现具有普适性的一般方法。他的整个认识论是，知识要靠无数个小步骤建构起来。 “科学如同自然，没有任何跨越。但要完成情形的过渡，只需要无限小的一个跳跃就足够了。”相比之下，约翰似乎总是横冲直撞。他拥有天才般的直觉，却没耐心去等一个缓缓到来的结果。

约翰并不理解，他自以为是的胜利没有任何意义。在这场争斗中，同在数学圈的家人们普遍站在了雅各布的一边。当哥哥依靠亲友和门徒的支持继续坐稳巴塞尔大学的教席，约翰却遭到排挤，被迫远赴荷兰。当然，格罗宁根大学的教授职位也很不错，但离家万里，且带着失意者的落寞。

1697年的平安夜里，他哀怨地写信给数学家皮埃尔·伐里农：“我有时刺伤哥哥，是因为我无法对他的苛待无动于衷，更没有懦弱到任由他把我踩在脚下；我努力摆脱他，我从不以任何方式依赖他，我从不欠他什么。”

遗憾

约翰在旅途中收到了哥哥去世的消息。在死于痛风并发症前，雅各布似乎预感到生命的衰亡，他在给雷布尼兹的信中写道：“如果我不久后将过世，我弟弟肯定会回到巴塞尔。他不会接受其他职位，他只想接替我的位子。”

没有人知道，约翰在收到死讯的一刻是何心情。但如哥哥所料，他转身回乡，代替雅各布成为巴塞尔大学的数学教授。

大戏已经落幕，但如同一个轮回，当孩子们一个个出生，约翰开始扮演起当初父亲的角色。他反对儿子们学习数学，逼迫他们经商。然后，他的儿子丹尼尔和当年的他一样固执，在巴塞尔大学攻读医学后，不久便转向数学，并成为家族中成就最大者。

约翰一生好斗，到了晚年愈发离谱。在因巴黎科学院大奖父子反目后，丹尼尔有意回避父亲的研究领域，约翰却有意去钻研丹尼尔熟悉的流体力学。当丹尼尔在1738年出版著作《流体力学》，约翰也紧随其后出版了一本《水力学》，并有意将写成时间注明为1732年。更糟的是，约翰实际上从儿子的书中盗用了素材。在日后一封写给欧拉的信中，丹尼尔义愤填膺：“我写出的《流体力学》从头到尾都不用感谢我父亲……我被抢劫了，失去了10年辛苦的成果。”

这不像是一个正常父亲的作为。事实上，约翰曾把自己的得意弟子欧拉送到圣彼得堡，去帮助丹尼尔度过艰难岁月，却难以接受多年后的青出于蓝。此情此景，多么像他与哥哥一生纠缠的重演。伯努利家族奉行的正是这样一条箴言：我乐于共享知识，但分摊荣耀却万万不可。

►丹尼尔·伯努利

莱比锡大学的数学教授鲁迪格·希勒认为，父亲的消极态度对兄弟两人的个性产生了不幸的影响。然而，作为弟弟的约翰受害尤其深重。1701年，34岁的约翰写信给父亲，口吻仍像一个求爱而不得的、伤心的孩子：“我从没收到过父亲的信，这说明你更喜欢哥哥们，对我没有感情。我真的不值得像哥哥那样被关心么?……你不允许我过自己想过的生活，而我已经将自己置于神的引导下。所以，请你不要来巴塞尔带走我的名誉，并说你与之毫无关系。”

或许是不被父亲认可的遗憾主宰了兄弟两人一生的命运，或许是对数学过于强烈的激情把伯努利家族引向偏执。将自己毕生的价值孤注一掷地砸在一门学科上，这必然带来生命的沉重，却也成就科学史上的辉煌。

雅各布一生的一句箴言，用拉丁语写就，就像伯努利家族共同的心结：我违父意，钻研群星。（Invito patre sidera verso. ）

参考文献：

1. Peiffer, Jeanne. “Jacob Bernoulli, teacher and rival of his brother Johann.” Journal Électronique d’Histoire des Probabilités et de la Statistique [electronic only] 2.1b (2006): Article-1.

2. 哈尔, 赫尔曼, and 范伟. 数学恩仇录: 数学家的十大论战. 复旦大学出版社, 2009.

3. 宋广利, 张韡, 刘树勇. 伯努利家族数学研究兴盛原因浅析[J]. 首都师范大学学报: 自然科学版, 2008, 29(4): 18-21.